Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 ta Trig Use the fundamental identities to simplify the expression cot beta sec beta I used 1tan^2u=secu since cot is the inverse of tan I flipped the tangent, then so it was 1 (1/tan)Integration of tan^2x sec^2x/ 1tan^6x dx Ask questions, doubts, problems and we will help you=> `1 2*tan^2x` It is seen that `sec^4 x tan^4 x = 1 tan^2 x` is not an identity, instead `sec^4x tan^4x = 1 2*tan^2xSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Power Reducing Formulas And How To Use Them With Examples Owlcation
5.25064634
5.25064634-Use \(\tan^2x=\sec^2x1~(=u^21)\) to replace the leftover tangents \(m\) is even or \(n\) is odd Use either \(1\) or \(2\) (both will work) The power of secant is odd and the power of tangent is even No guideline The integrals \(\ds\int\sec x\,dx\) and \(\ds\int\sec^3 x\,dx\) can usually be looked up, or recalled from memory Example 223What is the value of sin 3x?




Question Video Differentiating Functions Involving Trigonometric Ratios Using Pythagorean Identities Nagwa
In this video I go over the proof of the trigonometry identity tan^2(x) 1 = sec^2(x) The proof of this identity is very simple and like many other trig idYou just studied 17 terms! Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes
Question Please help me verify this equation cscx cscx =2sec^2x 1cscx 1cscx yes, the cscx's are over 1cscx and 1cscx Those are fractions So far i have gotten stuck on this porblem i have expanded csc x into 1/sinx in both parts of the left side ofTrig Identities Nice work!In this video, I go through a trigonometric proof which is1tan^2=sec^2The proof is fairly straight forward with some common knowledge of trigonometric fu
Let y = `tan^(1) (1cosx)/(sin x)` Then `=> y = tan^(1) ((2cos^2 x/2)/(2sin x/2,cos x/2))` `=> y = tan^1 (cot x/2)` `=> y = tan^1 {tan (pi/2 x/2)}`Get an answer for 'solve tan^2xsecx =1 in the range 0°≤x≤ 360°' and find homework help for other Math questions at eNotesCalculus 2, integral of (1tan^2x)/sec^2x, integral of cos(2x)




Which Of The Following Are Trigonometric Identitie Gauthmath




Question Video Differentiating Functions Involving Trigonometric Ratios Using Pythagorean Identities Nagwa
Free trigonometric identities list trigonometric identities by request stepbystep The identity, as you noted, is tan2x 1 = sec2x, for all values of x Rearranging, you absolutely get tan2x sec2x = 1 So, the original statement is falseTrigonometry Graph y=sec (2x) y = sec(2x) y = sec ( 2 x) Find the asymptotes Tap for more steps For any y = sec ( x) y = sec ( x), vertical asymptotes occur at x = π 2 n π x = π 2 n π, where n n is an integer Use the basic period for y = s e c ( x) y = s e c ( x), ( π 2, 3 π 2) ( − π 2, 3 π 2), to find the vertical




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube




Differentiate The Following From First Principle Tan 2x 1
Hi Simplifying the following (sec^2x csc^2x) (tan^2x cot^2x) tan^2x = sec^2x 1 cot^2x = csc^2x 1 (sec^2x csc^2x) (sec^2x 1 csc^2x 1)= 2Trigonometry sin (a/2)= square root of (1cos (a))/2 sin( a 2) = −√ 1 − cos(a) 2 sin ( a 2) = 1 cos ( a) 2 Since the radical is on the right side of the equation, switch the sides so it is on the left side of the equation −√ 1−cos(a) 2 = sin( a 2) 1 cos ( a) 2 = sin ( a 2) How many solutions of the equation $$\tan^2 x \sec^{10} x 1=0$$ lie in the interval $(0,10)$?




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube




The Derivative Of Sec2x Derivativeit
The cos2(2x) term is another trigonometric integral with an even power, requiring the powerreducing formula again The cos3(2x) term is a cosine function with an odd power, requiring a substitution as done before We integrate each in turn below ∫cos2(2x) dx = ∫ 1 cos(4x) 2 dx = 1 2 (x 1 4sin(4x)) CRewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x)Simplify and write the trigonometric expression in terms of sine and cosine (2tan^2x / sec^2x) 1 = (f (x))^2 f (x) =



2




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube
You ask for the formula of cot(AB) What you mean is the trigonometric identity of that ratio Tan^2 x1=sec^2x So to get 1 on the other side of the equal sign wouldn't it be sec^2xtan^2x=1?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!1 A water molecule is held together by two single polar covalent bonds False 2 Because oxygen has a greater electronegativity than hydrogen, water molecules are polar withFor each of the three trigonometric substitutions above we will verify that we can ignore the absolute value in each case when encountering a radical 🔗 For x = asinθ, x = a sin θ, the expression √a2 −x2 a 2 − x 2 becomes √a2−x2 = √a2−a2sin2θ= √a2(1−sin2θ)= a√cos2θ= acosθ = acosθ a 2 − x 2 = a 2 − a 2




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Int Tan 2x Secx 1 Dx Youtube
Trigonometry Square relation 2 deduction of sec^2x tan^2x = 1with worked out exampleCheck all that apply A cot^2xcsc2x=1 B sin^2xcos^2x=1 C sin^2x = 1 cos^2x D tan^2x = sec^2x1Now up your study game with Learn mode




Integral 1 Tan 2 X Sec 2 X Youtube



1
Free integral calculator solve indefinite, definite and multiple integrals with all the steps Type in any integral to get the solution, steps and graph Integral (tan^2x sec^2x)/(1tan^6x)dx Get the answers you need, now! Because if you take tan^2(x) 1 = sec^2(x) then tan^2(x) = sec^2(x) 1 And if we input that into the original then sec^2(x) * sin^2(x) sin^2(x) or tan^2(x)




If Y Tan 2x Sec 2x Find Dy Dx Brainly In



2
One to any power is one 1 cos2(x) 1 cos 2 ( x) Because the two sides have been shown to be equivalent, the equation is an identity 1sec2 (x)sin2(x) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers by µ • § ¶ ß ‹ › « » < > ≤ ≥ – — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° − ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ ∗ ∝ ∠ ´ ¸ ª º † ‡ À Á Â Ã Ä Å Æ Ç È É Ê Ë Ì Í Î Ï Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë ì í î ï ð ñ ò ó ô õ ö




Sec 6x Tan 6x 3sec 2xtan 2x 1 Solution



2
Tan^2xsec^2x/1tan^6x Ask questions, doubts, problems and we will help you True Start with the well known pythagorean identity sin^2x cos^2x = 1 This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identity Which of the following equations are identities?
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero
You could take tan(x) out of the fraction, but I still don't know how to go about simplifying it The book says the answer isIntegration of tan^2x sec^2x/ 1tan^6x dx Ask questions, doubts, problems and we will help youCos(3x) = 4cos^3(x) − 3cos(x) Here are some Important results * Pythagorean Identities sin 2X cos 2X = 1 1 tan 2X = sec 2X 1 cot 2X = csc 2X * Negative Angle Identities sin (X) = – sin X, odd function csc (X) = – csc X, odd function




How Many Can You Derive From First Principles Ppt Download




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
Found 2 solutions by ewatrrr, MathLover1 Answer by ewatrrr () ( Show Source ) You can put this solution on YOUR website!Prove that tan^2x sec^2x=1 Answers 3 Get Other questions on the subject Mathematics Mathematics, 14, klandry0 How long would it take to empty a pond that is 60x50x using a 1000 gallon pump Answers 3 continue Mathematics, 1730, iliketurtures In parallelogram abcd the ratio of ab to bcis 5 3 if the A few hints 1 sec x = 1/(cos x) 2 (sin x)/(cos x) = tan x That should give you a good start



Yorkshiremathstutor Com Wp Content Uploads 19 02 8 Differentiation Answers Pdf




Answered Let F X Tan 2x Which Of The Bartleby
Yes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 x Let us derive the equation We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomesI know that and The next step would then be to say that but now what?Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1



2



2
Viewed 24k times 1 I am trying to express this problem in terms of sin/cos and simplify I couldn't figure out where to go, I tried as best I could I know the answer is 1 but I am more interested to know how to do this problem tan 2 x − sec 2 If we are dealing with 'real' numbers, the sine function returns a value in the range 1, 1, thus, depending on what x is, the answer will be a number whose absolute value is less than or equal to one If you aren't



2




Tan 2x Formula What Is Tan 2x Formula Examples



Http Www Wssd Org Cms Lib02 Pa Centricity Domain 140 1 4 1 6 Pdf




Prove That Sec8x 1 Sec4x 1 Tan8x Tan2x




A Solution Of The Equation 1 Tan X 1 Tan X Sec 2x 2 Tan 2 0 Where X Lies In The Interval Pi2 Pi2 Is Given By




Trig Identity Sec2x Minus Tan2x T10 Youtube




Section 8 3 Trigonometric Integrals Ppt Download



What Is The Derivative Of Tan 1 Sec X Tan X Quora




Chapter 2 Answers
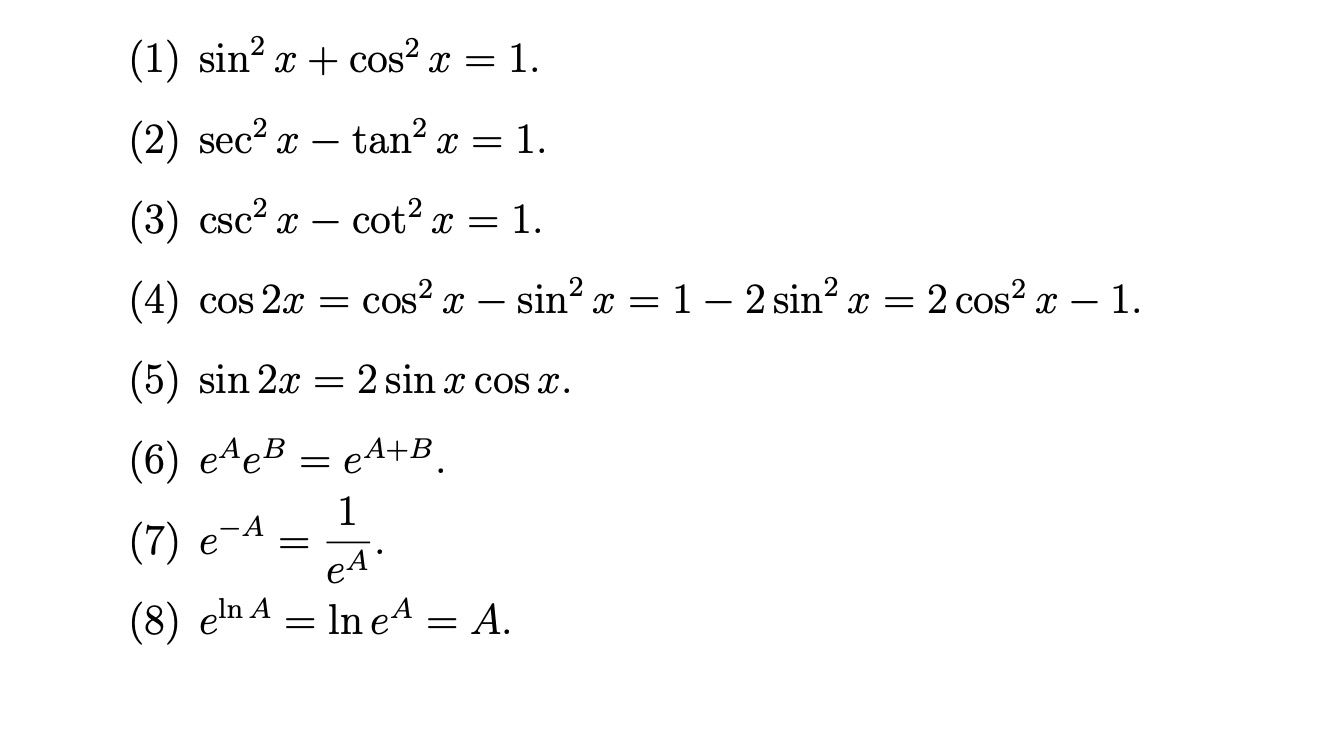



Here Is A List Of Identities Involving Trigonometric Chegg Com




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified




1 Cosx 1 Cosx Tan 2x Secx 1 2 Brainly In




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Sin2x Cos2x 1 Proof



Tan 2x Tan 2x



Http Www Math Brown Edu Tomg Formulas Pdf




Sec 6x Tan 6x 1 3 Tan 2x Sec 2x Brainly In




Lim X To 0 2 Tan X 2 Sin X X 2 Sin X Without L Hopital S Rule How Is My Procedure Wrong Mathematics Stack Exchange




Evaluate The Following Integral Sec 2x Tan 2x Dx Sec Chegg Com
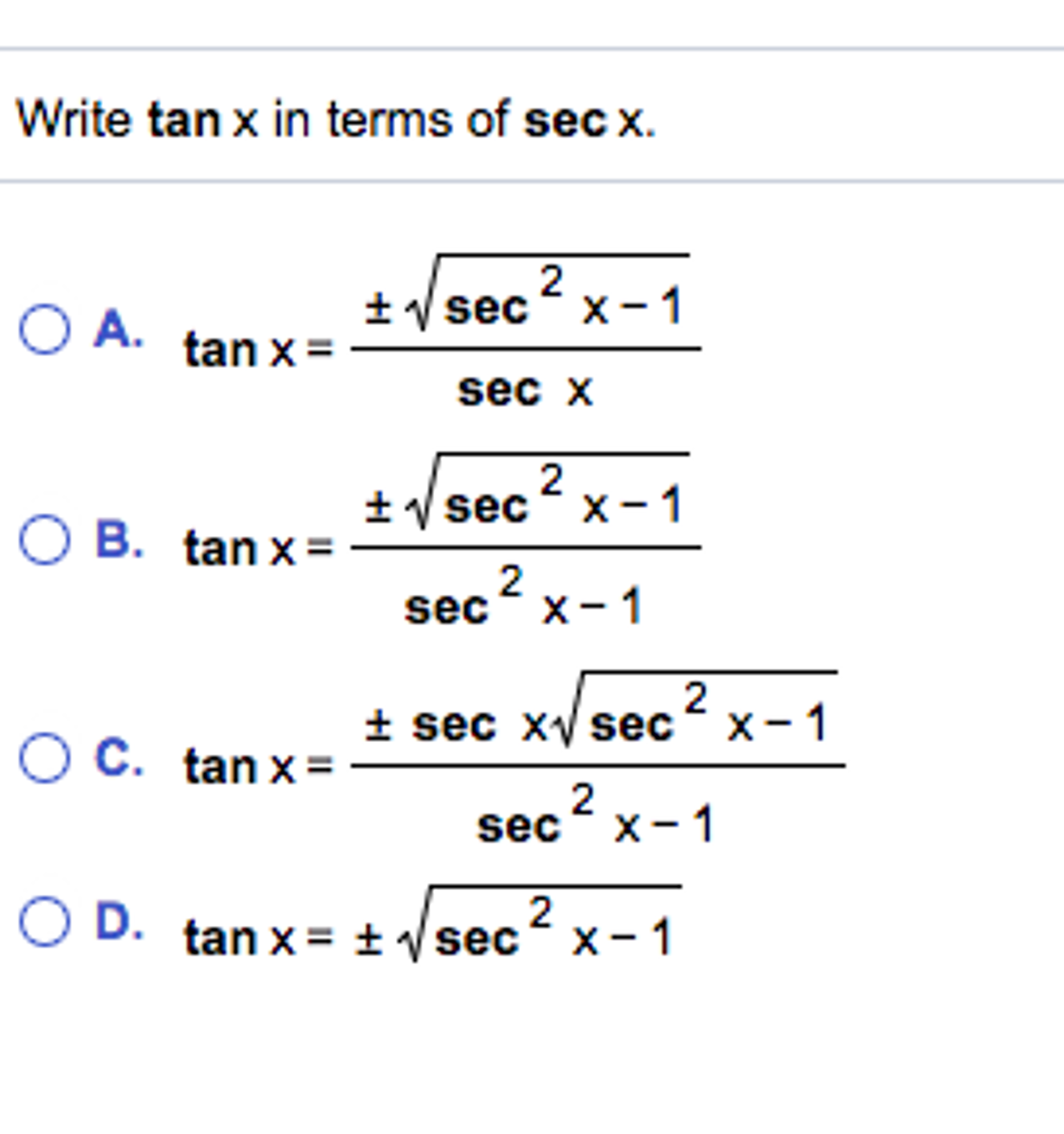



Write Tan X In Terms Of Sec X Tan X Plusminus Chegg Com




Question 34 Ssssd Maths Integrals Meritnation Com




The Value Of Int Tan 3 2x Sec 2x Dx Is Equal To




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



2




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Cos 2x
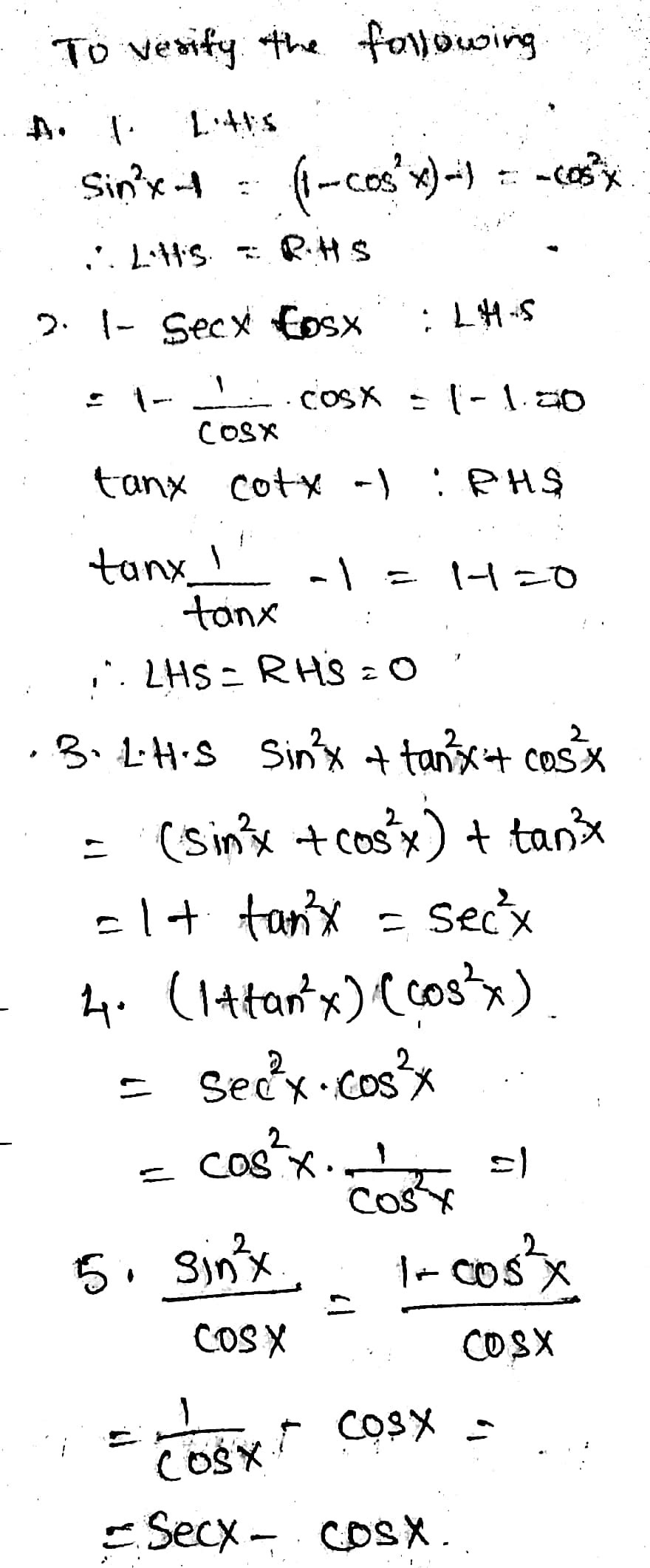



Directions Verify The Following Trigonometric Id Gauthmath




Ppt 5 1 Fundamental Trig Identities Powerpoint Presentation Free Download Id




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




How Many Can You Derive From First Principles Ppt Download
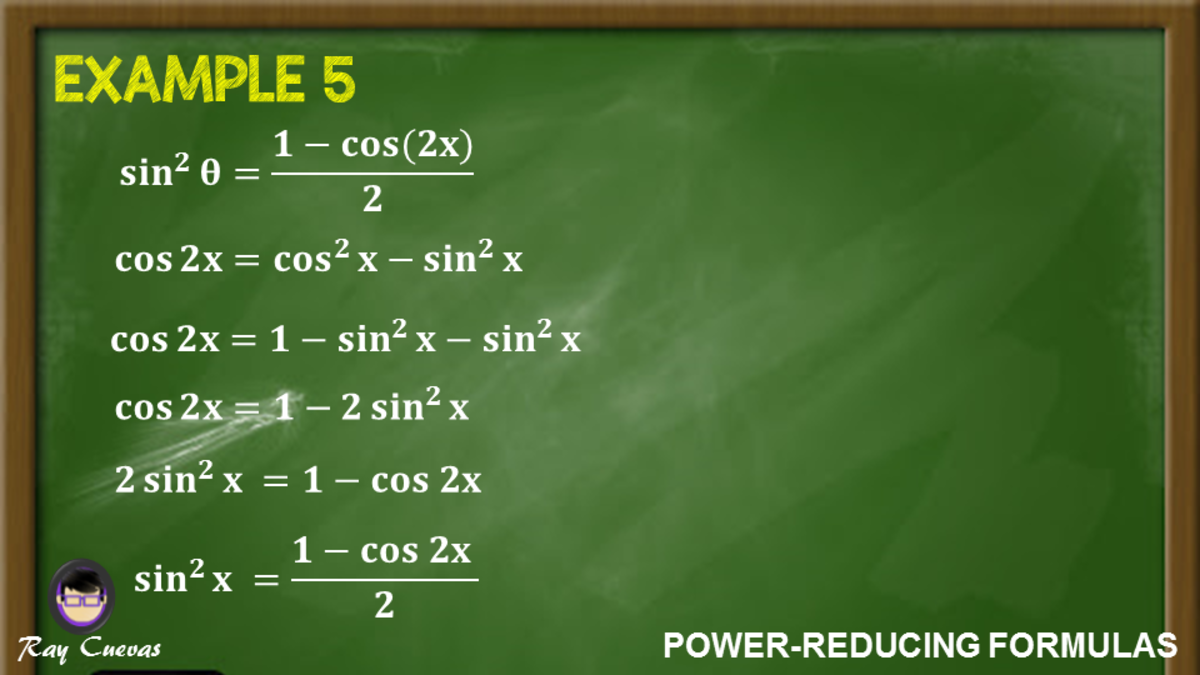



Power Reducing Formulas And How To Use Them With Examples Owlcation



2




Ppt Analytic Trig Powerpoint Presentation Free Download Id




Differential Equation D 2 1 Y E X Sec 2 X Tan X Mathematics Stack Exchange




Evaluate Lim Xrightarrow Frac Pi 2 Frac Tan 2x X Frac Pi 2 Orevaluate Lim Xrightarrow 3 Frac X 4 81 2x 2 5x 3 Snapsolve




Hs Trig Math Help Solving Trig Equations But I Don T Know How To Move Forward After Factoring Homeworkhelp




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Power Reducing Formulas And How To Use Them With Examples Owlcation




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
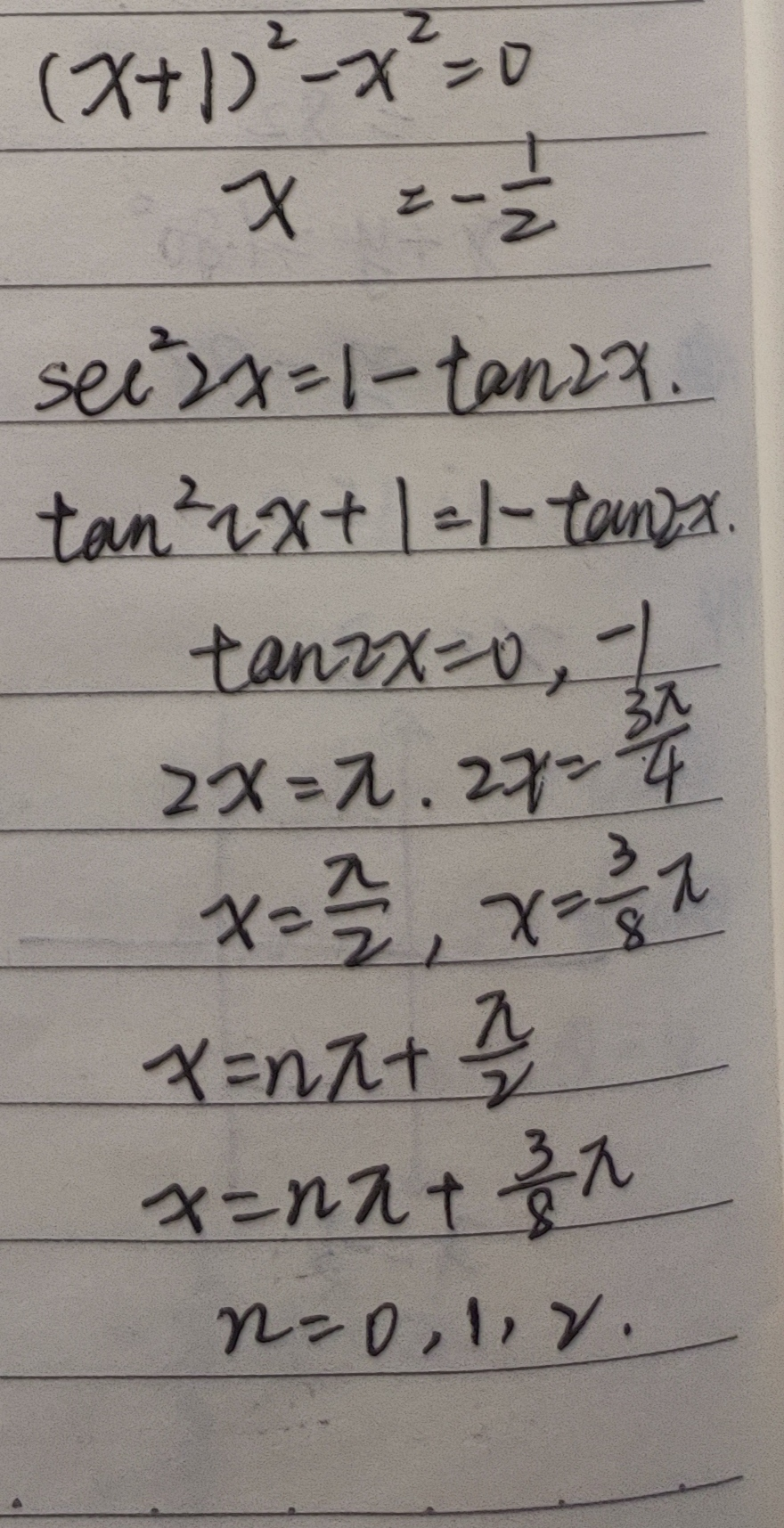



Sec 2 2x 1 Tan 2x Snapsolve



1



2




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Tan2x Sec2x ただの悪魔の画像



Tan 2x Tan 2x




Lim X Rightarrow Frac Pi 2 Frac Tan 2x Scholr
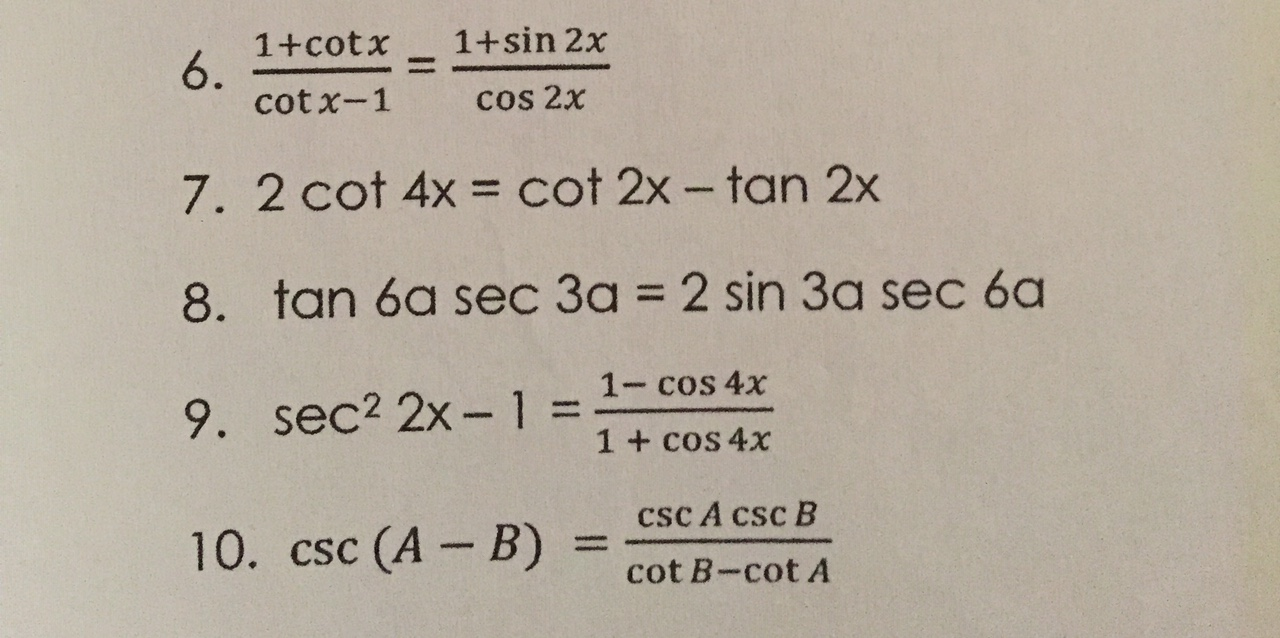



1 Cotx 1 Sin 2x 6 Cotx 1 Cos 2x 7 2 Cot 4x Cot 2x Chegg Com




1 Sin 2x Tan 2x Sec Sec 2 X Csc 2x 1 1 C Gauthmath



1




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic



Orion Math Iastate Edu Miriamc 8 2 Notes166 Sp17 Pdf




How Do You Integrate 1 Tan2x Sec2x Dx Socratic




Integration Trig Identities Ppt Download




Calameo Diapositivas Lenny Vanegas




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download




Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Calculus Mathematics Email Subject Lines




1 Cosx 1 Cosx Tan 2x Secx 1 2prove Brainly In




Derivative Of Sec 3 2x




If Tan 2 X Sec X A 0 Has Atleast One Solution Then Complete Set Of V Askiitians




Int Tanx Sec 2 X 1 Tan 2 X Dx




Answered If F X Tan 2x Then F X 3d Bartleby




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby



2
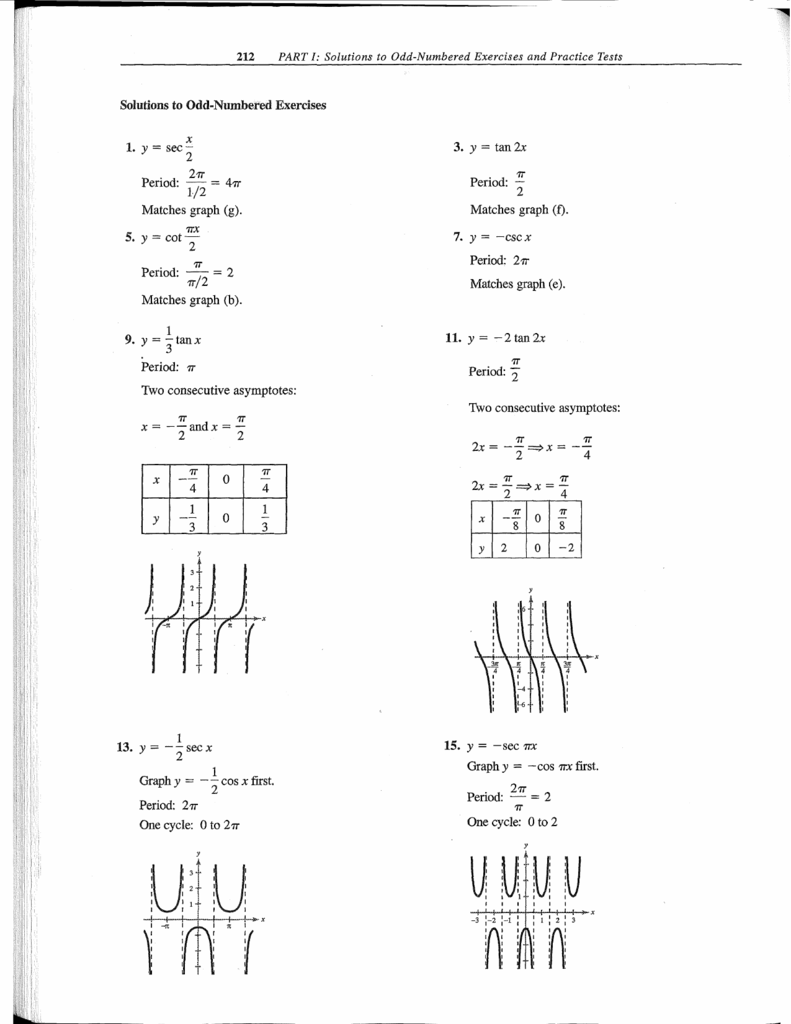



Solutions To Odd Number Exercises Lo Y Sec 2 Period
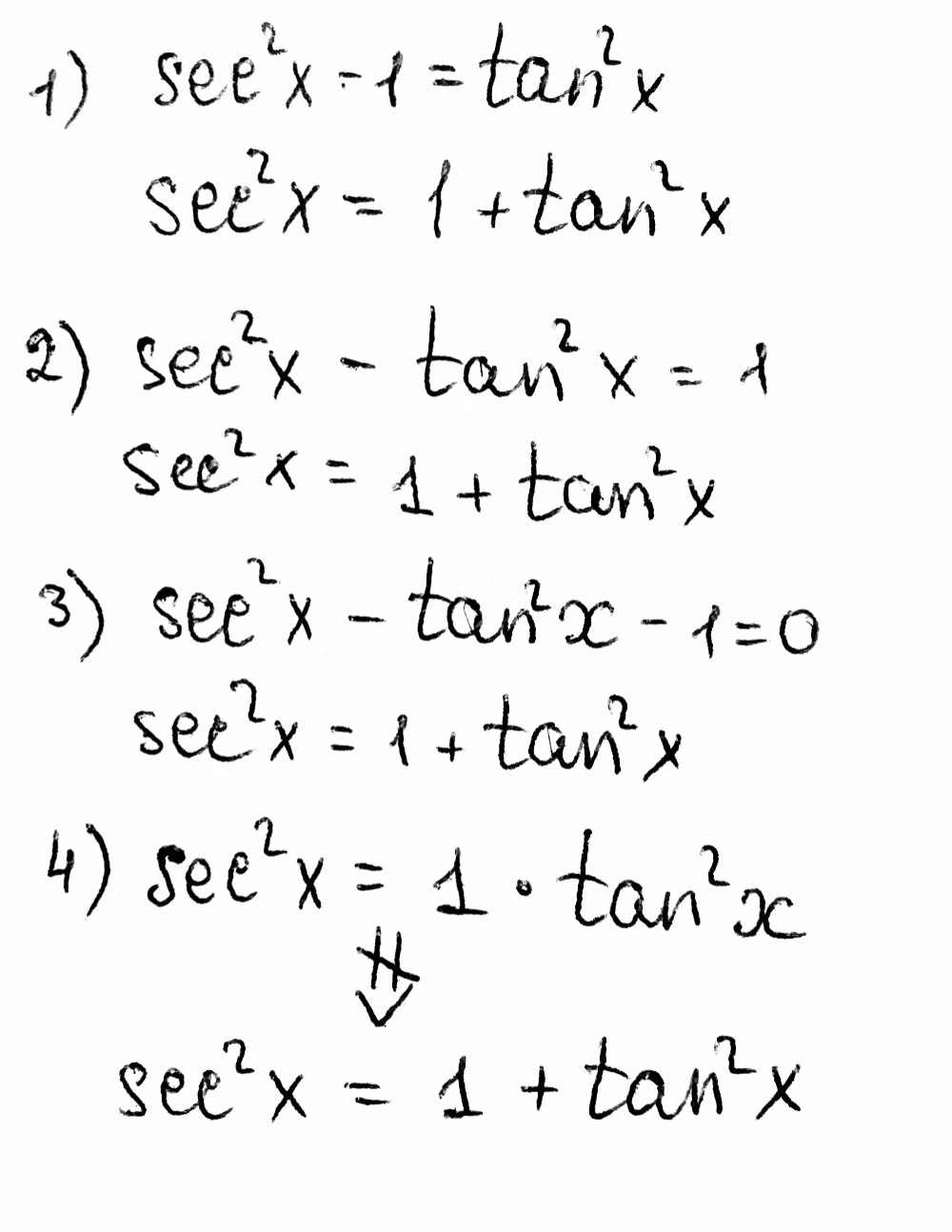



Which One Is Not Equivalent To Sec2x 1 Tan2x Sec Gauthmath



How To Integrate Secx A Btanx Quora




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic
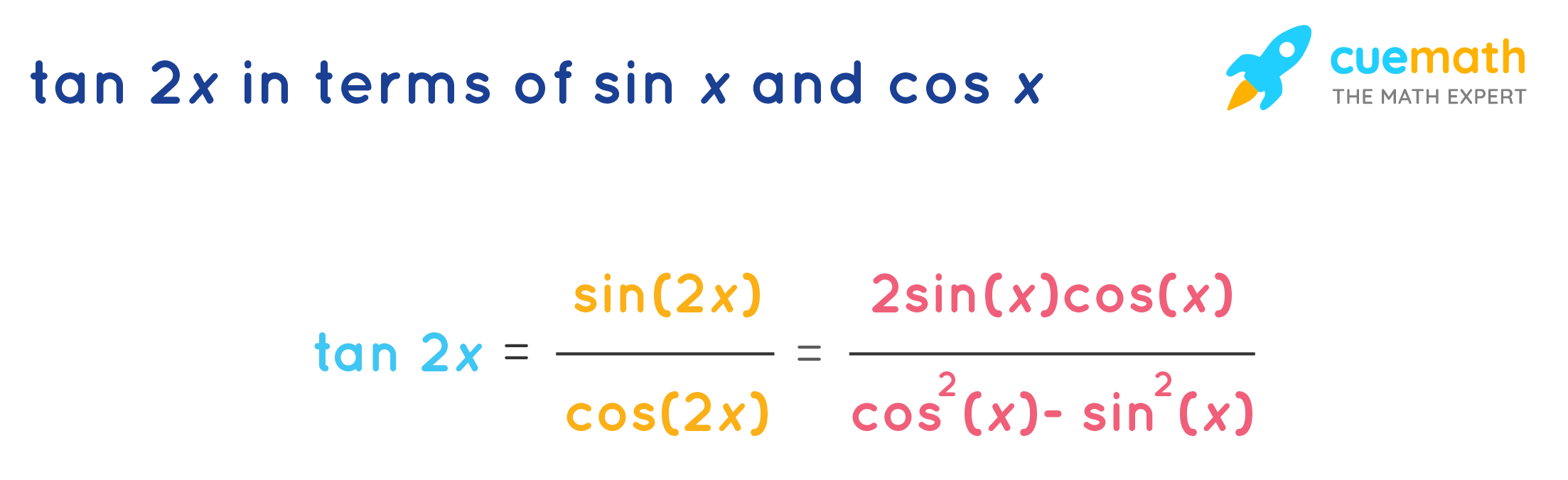



Tan 2x Formula What Is Tan 2x Formula Examples




Examples Int Tan 2x Sec 4x Dx




Find Integral X 2 Sin 2 X Sec 2 X 1 X 2 Teachoo




Question 1 Integrate The Following Function Sec 2x Chegg Com




I Int Sec 2x Tanxsqrt Tan 2x 1 Dx



2



1




Tan 2x 2tanx 5dy Dx 2 1 Tanx Sec 2x Differential Equations Brainly In



Http Www Stevejonak Com Test03 Addtional Review Pdf



2



Solved Evaluate The Derivatives Of The Following Functions With Respect To X And Simplify The Results 2 Points Each 1 Y 3 X 6 2 Y 2x 1 Course Hero




0 21 Solve By Inversion Method Y 1 0 22 Find The General Solution Of



0 件のコメント:
コメントを投稿